Красивая терминология является одним из достоинств современной криптографии. Названия панк-групп или ников на Tumbl - вот на что похожи криптографические термины, такие, как 'трудный предикат' (hard-core predicate), 'функция с секретом' (trapdoor function), или 'невозможный дифференциальный криптоанализ' (impossible differential cryptanalysis). Мне кажется, что еще более красиво звучит такой термин, как 'нулевое разглашение (zero knowledge)'.
Но красота термина 'нулевое разглашение' приводит к злоупотреблению им. Людям сразу кажется, что нулевое разглашение становится синонимом слов 'очень, очень безопасно'. Из-за этого данные слова добавляют к названиям систем безопасности и анонимных сетей – что на самом деле не имеет ничего общего с протоколом 'нулевое разглашение'.
Всё это мы сказали для того, чтобы подчеркнуть главное: доказательство с нулевым разглашением (zero knowledge proof) является одним из самых мощных инструментов криптографии из когда-либо разработанных. Но, к сожалению, оно относительно мало изучено. Попробуем дать не математическое объяснение того, что делает ZK (zero knowledge) таким особенным. Здесь мы будем говорить о некоторых актуальных протоколах ZK.
Происхождение нулевого разглашения
Понятие 'нулевое разглашение' было впервые предложено в 1980-х специалистами MIT Шафи Голдвассером, Сильвио Микали и Чарльзом Ракофф. (Shafi Goldwasser, Silvio Micali и Charles Rackoff). Эти исследователи работали над проблемой, которая относится к интерактивным системам доказательства - теоретическим системам, в которых первый участник (назовём его 'Испытатель' (Prover) обменивается сообщениями со вторым участником 'Контролёр' (Verifier) чтобы убедить контролёра, что некоторое математическое утверждение верно. *
До Голдвассера и других, большинство работ в этой области фокусировались на системах доказательства правильности. То есть, на случаях, когда злоумышленник - Испытатель пытается провернуть трюк с Контролёром, подсовывая ему ложное значение. Но Голдвассер, Микали и Ракофф рассмотрели противоположную сторону этой проблемы. Вместо того, чтобы беспокоится только об Испытателе, они спросили: что произойдёт, если вы не доверяете Контролёру?
Особо их обеспокоила возможность утечки информации. Конкретно, они задались вопросом, сколько дополнительной информации получит Контролёр в ходе доказательства самого факта, что утверждение верно?
Важно отметить, что это не просто теоретический интерес. Есть реальные, практические приложения, в которых эти вещи важны.
Вот одно из них: представьте, что клиент в реальном мире хочет войти на веб-сервер, используя пароль. Стандартный подход к проблеме 'в реальном мире' включает в себя хранение хэшированной версии пароля на сервере. Логин в такой системе рассматривается как вид 'подтверждения', что хэш предоставленного пароля это выход хэширующей функции действующего пароля. И, что более важно, как 'подтверждение' того, что клиент действительно знает пароль.
Большинство систем в реальном мире реализуют это 'подтверждение' наихудшим образом из возможных. Клиент просто передаёт оригинальный пароль на сервер, который повторно вычислят хэш пароля и сравнивает его с сохранённым значением. Проблема здесь очевидна: сервер получает мой пароль в самом притягательном для хакеров виде 'чистый текст'. А пользователь может только молится о том, что защита сервера не скомпрометирована.
То, что предложили Голдвассер, Микали и Ракофф, стало надеждой на появление новых методов подтверждения. В случае полной реализации, доказательства с нулевым разглашением смогут дать подтверждение в описанной выше задаче. При этом не разгласив ни одного бита информации, которая соответствует тому, что 'это утверждение верно'.
Пример из "реального мира"
До сих пор мы разговаривали о довольно абстрактных вещах. Давайте пойдём вперёд и приведём реальный пример (слегка безумный) для протокола 'нулевое разглашение'.
Чтобы мне было проще объяснить этот пример, давайте представим, что я магнат телекоммуникаций и нахожусь в процессе развёртывания новой сотовой сети. Моя сетевая структура представлена ниже на этом графе. Каждая вершина графа представляет собой мобильный передатчик, и соединяющие линии (грани) показывают места, где две соты перекрываются. В этих местах передатчики будут создавать друг другу помехи. Хорошо, что моя сетевая структура позволяет настроить каждую башню в одном из трёх частотных диапазонов, чтобы избежать такого влияния.
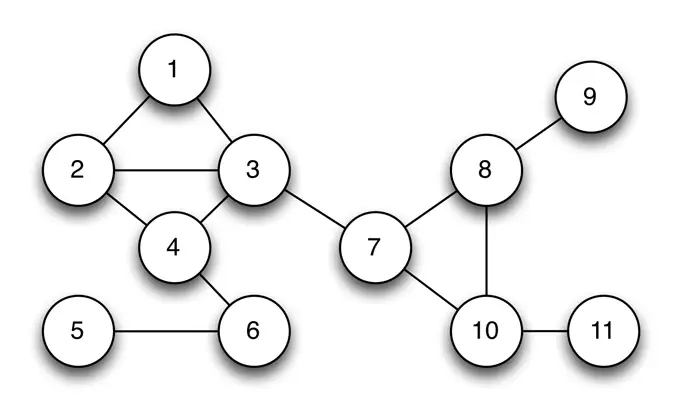
Таким образом, задача развёртывания моей сети сводится к тому, чтобы назначить свою полосу для каждой башни таким образом, чтобы клетки не пересекались. Если мы используем цвета для отображения частотных полос, то можем быстро разработать одно решение для этой проблемы:
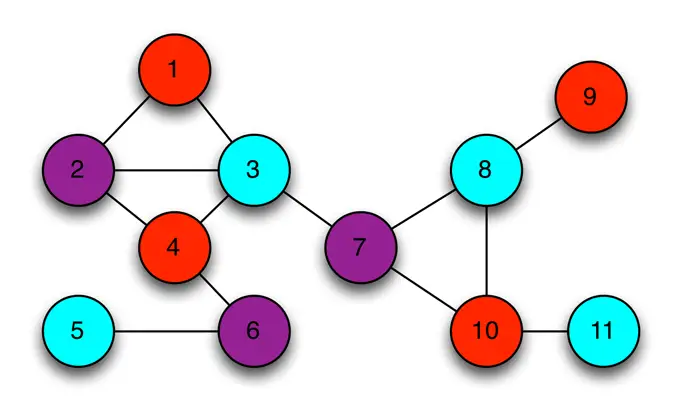
Конечно, многие из вас уже заметили. То, что я описал здесь — только частный случай знаменитой теоретической проблемы. Она носит название 'проблемы раскраски графа в три цвета'. Вы можете также знать об одной очень интересной особенности этой проблемы. Для некоторых графов очень трудно найти решение или даже определить, что такое решение существует. Задача раскраски графа в три цвета (и поиск ответа на вопрос, существует ли такое решение для данного случая), как известно, относятся к разряду NP-полных задач.
Само собой разумеется, что вышеописанные игрушечные загадки решить просто. Но если бы это не было так просто? Например, представьте, что моя сеть сотовой связи была очень большой и сложной. В этом случае мне бы не хватило вычислительной мощности, чтобы найти решение. В этом случае, было бы желательно поручить решение проблемы кому-нибудь ещё. Тому, у кого достаточно вычислительной мощности. Например, я мог бы попросить Google решить эту задачу.
Но есть одна проблема.
Предположим, что Google уделит мне столько, сколько нужно вычислительных мощностей для того, чтобы найти решение правильной раскраски моего графа. Я, конечно, не собираюсь платить им, пока не буду уверен в том, что у них есть это решение. В то же время, Google не собирается предоставить мне копию решения до тех пор, пока я не оплачу её. Мы в тупике.
В реальной жизни здравый смысл подсказывает нам ответ на эту дилемму, который включает в себя услуги юристов и эскроу-счета. Но здесь мы говорим не о реальной жизни, а о криптографии. И, если вы когда-нибудь читали работы криптографов, то уже знаете, что единственный способ найти решение проблемы — придумать полностью сумасшедшее техническое решение. Сумасшедшее техническое решение (со шляпами)
Представим, что сотрудники Google проконсультировались у Сильвио Микали из MIT, а он расспросил своих коллег Оде Голдрих (Oded Goldreich) и Ави Виджерсон (Avi Wigderson). Посоветовавшись, они разработали протокол, который настолько красив, что даже не требует компьютеров. Будет использоваться большой склад с запасом цветных карандашей и бумаги. Ещё понадобится большое количество шляп. **
Рассмотрим, как это работает
Сначала я войду в помещение склада и застелю пол бумагой, чтобы создать пространство для представления моей сотовой сети. Затем я покину склад. Google теперь может войти, перемешать коллекцию карандашей и выбрать три любых цвета (например, красный / голубой / фиолетовый, как в этом примере), и цвет, которым будет обозначено решение. Заметим, что какой конкретно цвет используется, значения не имеет.
Перед тем, как покинуть склад, Google накрывает каждую вершину шляпой. Когда я вернусь, это всё, что я увижу:
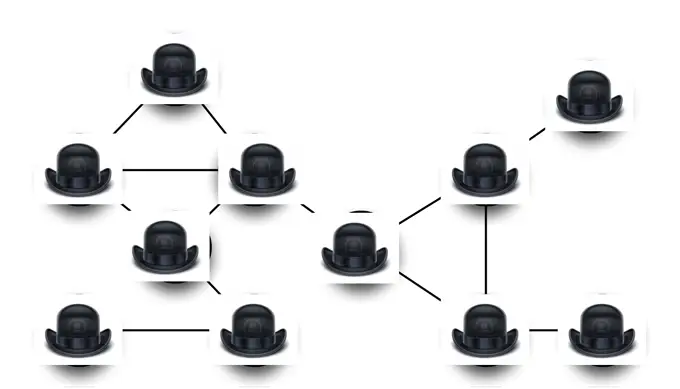
Очевидно, что такой подход отлично защитит секрет Google. Но это совсем не поможет мне. Возможно, Google заполняет цвета в случайном, а значит, в неправильном порядке. А может быть, они вообще не заполняли ничего.
Чтобы убедить меня в том, что задача действительно решалась, Google даёт мне возможность 'проверить' их результат раскраски графа. Я имею право выбрать, в случайном порядке, одну грань этого графа (то есть, по одной линии между двумя соседними шляпами). Google будет удалять эти две шляпы, показывая мне небольшую часть решения:
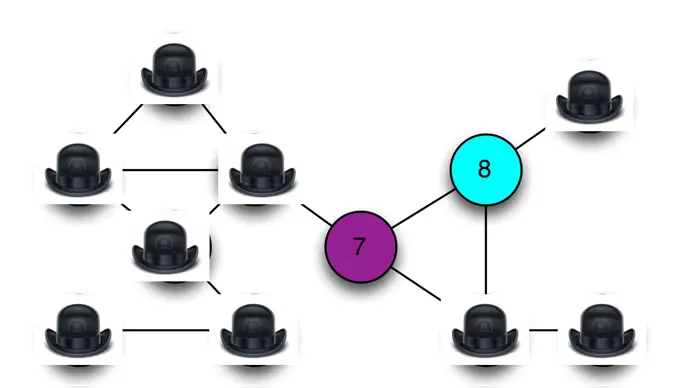
Обратите внимание, что у моего эксперимента есть два возможных исхода:
Если две показанные вершины имеют один и тот же цвет (или же вообще не окрашены!) тогда я точно буду уверен, что Google обманывает меня. В этом случае я не заплачу Google даже цента. Если две показанные вершины имеют различные цвета, значит, Google в этом случае не обманывает меня.
Надеюсь, первое утверждение очевидно. Второе потребует более подробного объяснения. Проблема в том, что если даже эксперимент был успешным, Google по-прежнему может обманывать меня. Всё-таки, я заглянул всего лишь под две шляпы. Если существует E различных рёбер в графе, то Google с большой долей вероятности может предоставить ошибочное решение. Например, после одного теста они обманывают меня с вероятностью (E-1) / E (что для 1000 граней будет составлять 99.9%).
К счастью, у Google есть ответ на этот вопрос. Мы просто запустим протокол снова!
Мы берём чистую бумагу для создания новой копии графа. Google теперь берёт новую случайную перетасовку трёх цветных карандашей. Затем они заполняют граф верным решением, но используя новый случайный набор трёх цветов.
Опять проводим операцию со шляпами. Я возвращаюсь, и в случайном порядке выбираю новые вершины. Ещё раз обратимся к логике, описанной выше. В этот раз, если всё пройдёт хорошо, я буду гораздо более уверен, что Google говорит мне правду. Это связано с тем, что, для того, чтобы обмануть меня, Google должно было повезти два раза.
Такое событие может произойти — но его вероятность будет ещё ниже. Вероятность того, что Google одурачит меня два раза подряд, составляет (E-1) / E * (E-1) / E (или около 99.8% вероятности для нашего примера с 1000 граней).
К счастью, мы не должны останавливаться на двух попытках. Мы будем пробовать снова и снова, пока не убедимся, что Google, с высокой долей вероятности, говорит правду.
Я призываю вас не верить мне на слово. Опробуйте этот Javascript, и убедитесь в этом самостоятельно.
Обратите внимание, что я никогда не уверен полностью, что Google честен – всегда остаётся крошечная вероятность, что они обманывают меня. Но, после большого количества итераций (E ^ 2, как в нашем случае) я в конце концов дойду до точки, в которой Google обманывает меня с пренебрежимо малой вероятностью – достаточной для применения на практике. После этого я спокойно могу отдать деньги Google.
Важно, что Google в этом случае также защищён. Если я попытаюсь узнать что-либо, сохраняя и анализируя заметки между запусками протокола, то потерплю неудачу Это вызвано тем, что Google при каждой итерации использует цвета, выбранные в случайном порядке. Ограниченная информация, которую я могу получить, не даст мне ничего. Для меня не существует способа связать эти данные воедино.
Что делает этот пример 'нулевым разглашением'?
Я пытаюсь убедить вас, что этот протокол не позволяет просочиться информации о решении Google. Но вам не нужно верить мне на слово! Первое правило криптографов заключается в том, чтобы никогда не верить таким вещам без доказательств.
Голдвассер, Микали и Ракофф предложили три критерия, которым должен отвечать каждый протокол 'нулевое разглашение'. Неформально их можно описать так:
Полнота. Если Google говорит мне правду, то я должен получить убедительные доказательства этого (доказательства с высокой вероятностью). Надёжность. Google может убедить меня только в том случае, если действительно говорит правду. 'Нулевое разглашение' (этот критерий действительно так и называется). Я не должен узнать ничего больше, кроме полученного решения Google.
Мы уже обсудили аргументы в пользу полноты. Протокол в конечном счёте убедит меня (с пренебрежимо малой вероятностью ошибки), если запустить его достаточное число раз. Надёжность тоже достаточно легко показать. Если Google попытается обмануть меня, я обнаружу это в подавляющем большинстве случаев.
Самым сложным свойством осталось 'нулевое разглашение'. Чтобы разобраться в нём, сделаем довольно странный мысленный эксперимент.
Мысленный эксперимент с машинами времени
Во-первых, давайте начнём с сумасшедшего предположения. Представим, что инженеры Google вовсе не так умны, как люди думают о них. Они работают над этой проблемой неделю за неделей, и им никак не удаётся найти решение. За двенадцать часов до окончания дедлайна в Google впадают в отчаяние. Они решают обмануть меня, и говорят, что у них есть раскраска для графа (хотя на самом деле её у них нет).
Их идея состоит в том, чтобы заглянуть в мастерскую GoogleX и позаимствовать на время прототип машины времени от Google. Первоначальным планом было отправиться на несколько лет назад и использовать дополнительное рабочее время на поиск новых решений проблемы. К сожалению, как и в случае с многими другими прототипами Google, машина времени имела ряд ограничений. Самое важное: она может отправиться во времени назад только на четыре с половиной минуты.
Таким образом, отпадает использование машины времени для увеличения времени на выполнение работы. Но всё-таки, оказалось, что эта весьма ограниченная технология может использоваться, чтобы обмануть меня.

Я действительно не знаю, что здесь происходит. Но кажется, это кстати.
План оказался дьявольски простым. Если Google не знает, каким образом должен быть окрашен граф, они просто случайным образом окрашивают бумагу, а затем накрывают вершины шляпами. Если, по счастливой случайности, вершины окажутся разных цветов, мы все вздохнём с облегчением и буде продолжать работу, считая, что всё нормально.
Предположим, я снимаю пару шляп и обнаруживаю две вершины одного и того же цвета. Если протокол реализован обычным образом, Google в этом случае потерпит фиаско. Но мы пользуемся машиной времени. Всякий раз, когда Google находит себя в неловком положении, он просто исправляет эту ситуацию. То есть, специально назначенный сотрудник Google дёргает рубильник, время перематывается назад на четыре с половиной минуты, и команда Google раскрашивает граф совершенно новым случайным решением. После этого они перематывают время вперёд и пробуют снова.
По сути, машина времени позволяет Google 'починить' любой неудачный вход в протокол таким образом, чтобы я ничего не заподозрил. Так как плохие результаты будут происходить только в 1/3 случаев, ожидаемое время выполнения протокола (с точки зрения Google) только незначительно больше, чем в случае честного выполнения протокола. С моей точки зрения, я даже не знаю, что эти путешествия во времени происходят.
Этот последний пункт является наиболее важным. С моей точки зрения, я одинаково взаимодействую с протоколом, есть машина времени или её нет. И всё же, стоит отметить ещё раз - в версии с машиной времени Google не имеет абсолютно никакой информации о том, как нужно раскрасить граф.
И что же из этого следует?
То, что мы только что показали — теоретический пример. В мире, где время бежит только вперёд, и никто не может обмануть меня с машиной времени, протокол с использованием шляп работает правильно. После E ^ 2 раундов его запуска я должен убедиться (не полностью, но с пренебрежимо малой вероятностью обмана), что граф окрашен правильно и Google обеспечил верную информацию.
Если же временем можно манипулировать (в частности, если Google может 'перемотать время'), то он может подделать протокол, даже если вообще не имеет информации о том, как должен быть окрашен граф.
С моей точки зрения, какая разница между этими двумя протоколами? Они имеют одинаковое статистическое распределение и передают одинаковое количество полезной информации.
Верьте или не верьте, это доказывает нечто очень важное.
В частности, предполагается, что я (Контролёр) (Verifier) имею какую-то стратегию, которая позволит 'извлечь' полезную информацию о том, как Google производит окрашивание, в случае запуска честного протокола. Тогда моя стратегия должна так же хорошо работать в том случае, если меня дурачат с машиной времени. Запуски протокола, с моей точки зрения, статистически идентичны. Я физически не могу показать разницу.
Таким образом, полностью идентично количество информации, которое я получу в 'реальном эксперименте' и 'эксперименте с машиной времени'. Количество информации, которое Google вкладывает в случае эксперимента с 'машиной времени', в точности равно нулю. Следовательно, даже в реальном мире не произойдёт утечки информации. Осталось только показать, что у компьютерщиков есть машина времени (тсс, это секрет).
Как избавиться от шляп и машин времени
Конечно, на самом деле мы не хотели бы запускать протокол, пользуясь шляпами. И даже у Google (скорее всего) нет настоящей машины времени.
Чтобы связать все эти вещи вместе ,нам нужно перенести этот протокол в цифровой мир. Для этого нам потребуется цифровой аналог 'шляпы': то, что скрывает цифровое значение, и в то же время 'связывает' значение и его создателя (создавая 'обязательство'), таким образом, чтобы он не мог изменить своё мнение.
К счастью, у нас есть прекрасный инструмент для этого приложения. Он называется цифровой схемой обязательства (digital commitment scheme). Схема обязательства позволяет одной из сторон создать для сообщения 'обязательство', сохраняя при этом его в секрете, а позже открыть 'обязательство', чтобы посмотреть, что внутри. Они могут быть построены из различных компонентов, в том числе из сильных криптографических функций хэширования.
Получив схему обязательства, мы собрали все компоненты, чтобы запустить в электронном виде протокол нулевого разглашения. Испытатель сначала кодирует окраску вершин в виде набора цифровых сообщений (например, числами 0, 1, 2), затем генерирует цифровые обязательства для каждой. Эти обязательства пересылаются для Контролёра. Когда Контролёр открывает один край, Испытатель показывает значения для обязательств, которые соответствуют двум вершинам.
Так нам удалось избавиться от шляп. Но как мы докажем, что этот протокол имеет нулевое разглашение?
Но мы ведь сейчас находимся в цифровом мире. Поэтому нам не нужна машина времени, чтобы подтвердить то, что протокол работает. Ключевая хитрость заключается в том, что протокол будет работать не между двумя людьми, а между двумя различными компьютерными программами (или, говоря более формально, двумя вероятностными машинами Тьюринга (probabilistic Turing machines.)
Сейчас мы можем доказать следующую теорему: если Контролёр собирается извлечь полезную информацию при обычном запуске протокола, он получит то же количество полезной информации, что и при 'обманном' запуске протокола, где Испытатель не вложил никакой информации с самого начала.
Мы с вами говорим о компьютерных программах, а они умеют 'возвращаться назад во времени'. Например, рассмотрим возможность использования виртуальной машины, которая умеет делать моментальные снимки. Пример 'перемотки времени' с использованием виртуальных машин. Первоначально виртуальная машина идёт по одному пути, возвращается к исходному состоянию, затем выполнение разветвляется на новый путь.
Даже если не рассматривать виртуальные машины, любую компьютерную программу можно 'перемотать' к предыдущему состоянию, просто запустив программу с самого начала и послав на вход те же самые данные. При условии, что входы, (в том числе ввод случайных чисел), фиксированы, программа всегда будет следовать по одному и тому же пути выполнения. Так мы можем перемотать программу, запустив её со старта и 'разветвив' её выполнение, когда программа достигнет некоторой нужной точки.
В конечном счёте, то, что мы получаем, можно представить в виде теоремы. Если для Контролёра существует компьютерная программа, которая успешно извлекает полезную информацию от Испытателя (интерактивно работая с протоколом), то Испытатель может использовать трюк с перемоткой программы, подсовывая Контролёру случайные решения. Используется логика, которую мы уже применяли выше: если Контролёр успешно может извлечь информацию, запустив реальный протокол, значит, он получит то же количество информации, запустив поддельный протокол, основанный на перемотке программы назад. Но так как поддельный протокол не передаёт полезных данных, нет никакой информации, которую можно извлечь. Таким образом, информация, которую может извлечь Контролёр, всегда равняется нулю.
Что же из этого всего следует?
Подытожив, можно сказать, что протокол является полным и надёжным. О надёжности можно говорить в любой ситуации, в которой обе стороны не пытаются обмануть друг друга.
В то же время, протокол имеет нулевое разглашение. Чтобы доказать это, мы показали, что программа, которую запускает Контролёр для извлечения информации, будет в состоянии извлечь данные из программы, в которой нет осмысленных данных. Это приводит к очевидному противоречию, которое говорит нам, что протокол в любой ситуации не имеет утечек информации.
Это даёт нам важные преимущества. Так как любой может создать поддельную запись протокола, (как в примере с Google, когда они пытались убедить меня, что у них есть решение), я не могу переиграть запись протокола, чтобы доказать свою правоту кому-либо ещё (например, судье). Судья скажет, что не уверен в том, что запись сделана честно и не отредактирована (как в примере с Google и использованием машины времени). Это означает, что стенограмма протокола сама по себе не содержит никакой информации. Протокол имеет смысл только, если я сам принимал участие, и могу быть уверенным, что всё происходило в реальном времени.
Доказательства для всех NP!
Для тех, кто добрался до этого момента, у меня есть важные новости. Задача раскраски сотовой сети в три цвета является интересной сама по себе, но это ещё не всё. По-настоящему интересная вещь о задаче раскраски в три цвета — то, что она относится к классу NP-полных. А это значит, что любая другая проблема, которая относится к классу NP, может быть сведена к этой.
Проще говоря, Голдрих, Микали и Виджерсон доказали, что 'эффективные' ZK существуют для обширного класса полезных задач. Многие из них являются гораздо более интересными, чем задача о присвоении частот в сотовой сети.
Вы просто находите утверждение (в NP) которое хотите проверить, и переводите его в проблему раскраски графа в три цвета. С этой точки вы можете запустить цифровую версию нашего протокола со шляпами.
Вместо итогов
Конечно, сразу начать использовать этот протокол на практике было бы безумно глупо. Его вычислительная стоимость будет включать в себя общий размер первоначального заявления и свидетельства, плюс стоимость перевода задачи в граф, и ещё E ^ 2 запусков протокола, которые необходимы для того, чтобы убедиться в правильности решения. Теоретически это 'эффективно', но так как общая стоимость доказательства будет многочленом от длины входа, на практике это не применимо.
Так что мы пока что доказали только то, что такие доказательства возможны. Осталось найти такие доказательства, которые являются достаточно практичными для реального использования.
Примечания
* Формально, целью интерактивного доказательства является убеждение Контролёра, что определённая строка принадлежит какому-либо языку. Обычно Испытатель в задачах имеет неограниченную мощность, а Контролёр ограничен в возможности расчётов.
** Этот пример основан на оригинальном решении Голдвассера, Микали и Ракофф, и учебном примере с использованием шляп, который разработал Сильвио Микали.
****** Простой пример обязательства может быть построен с использованием примера хэширующей функции. Для создания обязательства значения "x" мы просто генерируем некоторую (достаточно длинную) строку случайных чисел, которую назовём 'соль', и выходное обязательство C = хэш (соль || x). Чтобы открыть обязательство, вы просто открываете 'x' и 'соль'. Любой желающий может проверить, что первоначальное обязательство действует, пересчитав хэш повторно. Это безопасный метод при некоторых, умеренно сильных, предположениях о самой функции.


